12. Applications of Taylor Series

Exercises

a. Limits

1

Use a power series to compute each limit.

1. \(\displaystyle \lim_{x\to0}\dfrac{e^{2x}-1-2x-2x^2}{x^3}\)

   \(\displaystyle \lim_{x\to0}\dfrac{e^{2x}-1-2x-2x^2}{x^3} =\dfrac{4}{3}\)

   We start with the series: \[ e^x=\sum_{n=0}^\infty \dfrac{x^n}{n!} =1+x+\dfrac{x^2}{2}+\dfrac{x^3}{6}++\dfrac{x^4}{24}\cdots \] We make the substitution \(x\to 2x\): \[ e^{2x}=\sum_{n=0}^\infty \dfrac{(2x)^n}{n!} =1+2x+\dfrac{4x^2}{2}+\dfrac{8x^3}{6}+\dfrac{16x^4}{24}+\cdots \] We substitute this into the limit and simplify: \[\begin{aligned} \lim_{x\to0} &\dfrac{e^{2x}-1-2x-2x^2}{x^3} \\ &=\lim_{x\to0} \dfrac{\left(1+2x+\dfrac{4x^2}{2}+ \dfrac{8x^3}{6}+\dfrac{16x^4}{24}+\cdots \right)-1-2x-2x^2}{x^3} \\ &=\lim_{x\to0} \dfrac{\left(\dfrac{8x^3}{6}+\dfrac{16x^4}{24}+\cdots\right)}{x^3} =\lim_{x\to0}\left(\dfrac{8}{6}+\dfrac{16x}{24}+\cdots\right) =\dfrac{4}{3} \end{aligned}\]

2. \(\displaystyle \lim_{x\to0}\dfrac{1-\cos(x^2)}{x^4}\)

   \(\displaystyle \lim_{x\to0}\dfrac{1-\cos(x^2)}{x^4} = \dfrac{1}{2}\)

   We start with the series: \[ \cos x =\sum_{k=0}^\infty (-1)^k\dfrac{x^{2k}}{(2k)!} =1-\dfrac{x^2}{2}+\dfrac{x^4}{24}-\cdots \] We make the substitution \(x\to x^2\): \[\begin{aligned} \cos(x^2) &=\sum_{k=0}^\infty (-1)^k\dfrac{x^{4k}}{(2k)!} =1-\dfrac{x^4}{2}+\dfrac{x^8}{24}-\cdots \end{aligned}\] We substitute this into the limit and simplify: \[\begin{aligned} \lim_{x\to0} &\dfrac{1-\cos(x^2)}{x^4} =\lim_{x\to0} \dfrac{1-\left(1-\dfrac{x^4}{2}+\dfrac{x^8}{24}-\cdots\right)}{x^4} \\ &=\lim_{x\to0} \dfrac{\dfrac{x^4}{2}-\dfrac{x^8}{24}+\cdots}{x^4} \\ &=\lim_{x\to0}\left(\dfrac{1}{2}-\dfrac{x^4}{24}+\cdots\right) =\dfrac{1}{2} \end{aligned}\]

3. \(\displaystyle \lim_{x\to0}\dfrac{1-x^2-\cos^2x}{x^4}\)

   Recall: \[ \cos^2 x=\dfrac{1+\cos(2x)}{2} \]

   \(\displaystyle \lim_{x\to0}\dfrac{1-x^2-\cos^2x}{x^4}=\dfrac{-1}{3}\)

   First recall: \[ \cos^2 x=\dfrac{1+\cos(2x)}{2} \] So we substitute \(x\to2x\) into the series: \[ \cos x =1-\dfrac{x^2}{2}+\dfrac{x^4}{24}-\cdots \] to get: \[\begin{aligned} \cos(2x) &=1-\dfrac{4x^2}{2}+\dfrac{16x^4}{24}-\cdots \\ &=1-2x^2+\dfrac{2x^4}{3}-\cdots \end{aligned}\] So: \[\begin{aligned} \cos^2x&=\dfrac{1+\cos(2x)}{2} \\ &=\dfrac{1+1-2x^2+\dfrac{2x^4}{3}-\cdots}{2} \\ &=1-x^2+\dfrac{x^4}{3}-\cdots \\ \end{aligned}\] We substitute this into the limit and simplify: \[\begin{aligned} \lim_{x\to0} &\dfrac{1-x^2-\cos^2x}{x^4} \\ &=\lim_{x\to0} \dfrac{1-x^2-\left(1-x^2+\dfrac{x^4}{3}-\cdots\right)}{x^4} \\ &=\lim_{x\to0} \dfrac{-\dfrac{x^4}{3}+\cdots}{x^4} \\ &=\lim_{x\to0}\left(-\dfrac{1}{3}+\cdots\right) =\dfrac{-1}{3} \end{aligned}\]

4. \(\displaystyle \lim_{x\to0}\dfrac{1-\cos^2x}{x^4}\)

   \(\displaystyle \lim_{x\to0}\dfrac{1-\cos^2x}{x^4} =\infty\)

   In the previous problem we found: \[ \cos^2x=1-x^2+\dfrac{x^4}{3}-\cdots \] We substitute this into the limit and simplify: \[\begin{aligned} \lim_{x\to0}\dfrac{1-\cos^2x}{x^4} &=\lim_{x\to0} \dfrac{1-\left(1-x^2+\dfrac{x^4}{3}-\cdots \right)}{x^4} \\ &=\lim_{x\to0}\dfrac{x^2-\dfrac{x^4}{3}+\cdots}{x^4} \\ &=\lim_{x\to0}\left(\dfrac{1}{x^2}-\dfrac{1}{3}+\cdots\right) =\infty \end{aligned}\]

5. \(\displaystyle \lim_{x\to0}\dfrac{1-\cos^2x}{x^2}\)

   \(\displaystyle \lim_{x\to0}\dfrac{1-\cos^2x}{x^2}=1\)

   In a previous problem we found: \[ \cos^2x=1-x^2+\dfrac{x^4}{3}-\cdots \] We substitute this into the limit and simplify: \[\begin{aligned} \lim_{x\to0}\dfrac{1-\cos^2x}{x^2} &=\lim_{x\to0} \dfrac{1-\left(1-x^2+\dfrac{x^4}{3}-\cdots \right)}{x^2} \\ &=\lim_{x\to0}\dfrac{x^2-\dfrac{x^4}{3}+\cdots}{x^2} \\ &=\lim_{x\to0}\left(1-\dfrac{1}{3}x^2+\cdots\right) =1 \end{aligned}\]

   This was the hard way to do this problem. \[\begin{aligned} \lim_{x\to0} \dfrac{1-\cos^2x}{x^2} &=\lim_{x\to0} \dfrac{\sin^2x}{x^2} \\ &=\left(\lim_{x\to0} \dfrac{\sin x}{x}\right)^2 =1 \end{aligned}\]

6. \(\displaystyle \lim_{x\to0} \dfrac{x-\ln(1+x)}{x^2}\)

   \(\displaystyle \lim_{x\to0} \dfrac{x-\ln(1+x)}{x^2} =\dfrac{1}{2}\)

   We substitute the series: \[ \ln(1+x)=\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n}x^n =x-\dfrac{x^2}{2}+\cdots \] into the limit and simplify: \[\begin{aligned} \lim_{x\to0} &\dfrac{x-\ln(1+x)}{x^2} \\ &=\lim_{x\to0} \dfrac{x-\left(x-\dfrac{x^2}{2}+\cdots\right)}{x^2} =\dfrac{1}{2} \end{aligned}\]

7. \(\displaystyle \lim_{x\to0}\dfrac{\sin x-x\cos x}{x^3}\)

   \(\displaystyle \lim_{x\to0} \dfrac{\sin x-x\cos x}{x^3} =\dfrac{1}{3}\)

   We substitute the two series: \[ \cos x=1-\dfrac{x^2}{2}+\cdots \qquad \sin x=x-\dfrac{x^3}{6}+\cdots \] into the limit and simplify: \[\begin{aligned} \lim_{x\to0} &\dfrac{\sin x-x\cos x}{x^3} \\ &=\lim_{x\to0} \dfrac{\left(x-\dfrac{x^3}{6}+\cdots\right) -x\left(1-\dfrac{x^2}{2}+\cdots\right)}{x^3} \\ &=\lim_{x\to0} \dfrac{-\dfrac{x^3}{6}+\dfrac{x^3}{2}+\cdots}{x^3} \\[5pt] &=\lim_{x\to0}\left(-\dfrac{1}{6}+\dfrac{1}{2}+\cdots\right) =\dfrac{1}{3} \end{aligned}\]

b. Derivatives

1

8. Let \(f(x)=\cos(x^2)\).

   1. Compute \(f^{(16)}(0)\).

      Compare the coefficient of \(x^{16}\) in the series for \(\cos(x^2)\) to that in the general Maclaurin series.

      \(\displaystyle f^{(16)}(0)=\dfrac{16!}{8!}\)

      The coefficient of \(x^{16}\) in the general Maclaurin series: \[ f(x)=\sum_{n=0}^\infty \dfrac{f^{(n)}(0)}{n!}x^n =f(0)+f'(0)x+\dfrac{f''(0)}{2}x^2+\cdots \] is \(\dfrac{f^{(16)}(0)}{16!}\). To find the series for \(\cos(x^2)\) substitute \(x\to x^2\) in the series \[ \cos x=\sum_{k=0}^\infty (-1)^k\dfrac{x^{2k}}{(2k)!} =1-\dfrac{x^2}{2}+\dfrac{x^4}{24}-\cdots \] to get \[ \cos(x^2)=\sum_{k=0}^\infty (-1)^k\dfrac{x^{4k}}{(2k)!} =1-\dfrac{x^4}{2}+\dfrac{x^8}{24}-\cdots \] The power of \(x\) is \(4k\). This is \(16\) when \(k=4\). So the coefficient of \(x^{16}\) is \(\dfrac{(-1)^4}{8!}\). Equate coefficients and solve: \[ \dfrac{f^{(16)}(0)}{16!}=\dfrac{1}{8!} \qquad \Longrightarrow \qquad f^{(16)}(0)=\dfrac{16!}{8!} \]

   2. Compute \(f^{(18)}(0)\).

      \(\displaystyle f^{(18)}(0)=0\)

      The coefficient of \(x^{18}\) in the Maclaurin series: \[ f(x)=\sum_{n=0}^\infty \dfrac{f^{(n)}(0)}{n!}x^n =f(0)+f'(0)x+\dfrac{f''(0)}{2}x^2+\cdots \] is \(\dfrac{f^{(18)}(0)}{18!}\). To find \(f^{(18)}(0)\), we need to equate this to the coefficient of \(x^{18}\) in the series \[ \cos(x^2)=\sum_{k=0}^\infty (-1)^k\dfrac{x^{4k}}{(2k)!} =1-\dfrac{x^4}{2}+\dfrac{x^8}{24}-\cdots \] The power of \(x\) is \(4k\). When is this \(18\)? Never! So the coefficient of \(x^{18}\) is \(0\) and \(f^{(18)}(0)=0\).

9. Let \(g(x)=x^2\ln(1+x)\).

   1. Compute \(f^{(14)}(0)\).

      Look for the coefficient of \(x^{14}\) in the series for \(x^2\ln(1+x)\).

      \(\displaystyle g^{(14)}(0)=\dfrac{-14!}{12}\)

      The coefficient of \(x^{14}\) in the general Maclaurin series: \[ f(x)=\sum_{n=0}^\infty \dfrac{f^{(n)}(0)}{n!}x^n =f(0)+f'(0)x+\dfrac{f''(0)}{2}x^2+\cdots \] is \(\dfrac{f^{(14)}(0)}{14!}\). To find the series for \(x^2\ln(1+x)\) we multiply the series \[ \ln(1+x)=\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n}x^n =x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\cdots \] by \(x^2\) to get \[ x^2\ln(1+x)=\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n}x^{n+2} =x^3-\dfrac{x^4}{2}+\dfrac{x^5}{3}-\cdots \] The power of \(x\) is \(n+2\). This is \(14\) when \(n=12\). So the coefficient of \(x^{14}\) is \(\dfrac{-1}{12}\). Equate coefficients and solve: \[ \dfrac{f^{(14)}(0)}{14!}=\dfrac{-1}{12} \qquad \Longrightarrow \qquad f^{(14)}(0)=\dfrac{-14!}{12} \]

   2. Compute \(f^{(15)}(0)\).

      \(\displaystyle f^{(15)}(0)=\dfrac{15!}{13}\)

      To find \(f^{(15)}(0)\), we need to equate the coefficient of \(x^{15}\) in the general Maclaurin series: \[ f(x)=\sum_{n=0}^\infty \dfrac{f^{(n)}(0)}{n!}x^n =f(0)+f'(0)x+\dfrac{f''(0)}{2}x^2+\cdots \] to the coefficient of \(x^{15}\) in the series \[ x^2\ln(1+x)=\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n}x^{n+2} =x^3-\dfrac{x^4}{2}+\dfrac{x^5}{3}-\cdots \] The power of \(x\) is \(n+2\). When is this \(15\)? When \(n=13\). So the coefficient of \(x^{15}\) is \(\dfrac{1}{13}\). Equate coefficients and solve: \[ \dfrac{f^{(15)}(0)}{15!}=\dfrac{1}{13} \qquad \Longrightarrow \qquad f^{(15)}(0)=\dfrac{15!}{13} \]

c. Integrals

1

2

10. Consider the function \(\displaystyle f(x)=\int_0^x \dfrac{1-e^{-t}}{t}\,dt\).

    1. Find the Maclaurin series for \(f(x)\).

       Start with the series for \(e^{-t}\).

       \(\displaystyle f(x)=\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n!}\dfrac{x^n}{n}\)

       We start with the series for \(e^{-t}\): \[ e^{-t}=\sum_{n=0}^\infty \dfrac{(-t)^n}{n!} =1+\sum_{n=1}^\infty \dfrac{(-1)^n}{n!}t^n \] So: \[ 1-e^{-t}=\sum_{n=1}^\infty \dfrac{(-1)^{n+1}}{n!}t^n \] Diving by \(t\), we get: \[ \dfrac{1-e^{-t}}{t}=\sum_{n=1}^\infty \dfrac{(-1)^{n+1}}{n!}t^{n-1} \] We now integrate. \[\begin{aligned} f(x)&=\int_0^x \dfrac{1-e^{-t}}{t}\,dt =\int_0^x \sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n!}t^{n-1}\,dt \\ &=\left[\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n!}\dfrac{t^n}{n}\right]_0^x =\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n!}\dfrac{x^n}{n} \end{aligned}\] Since this is a definite integral, we don't need any \(+C\) but we do need to check the lower limit which here came out to \(0\).

    2. Approximate \(f(0.1)\) by the Maclaurin polynomial of degree \(3\) for \(f(x)\).

       \(\displaystyle f(0.1)\approx.097\,556\)

       The Maclaurin series for \(f(x)\) is: \[ f(x)=\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n!}\dfrac{x^n}{n} \] The Maclaurin polynomial of degree \(3\) is: \[ f(x)\approx\sum_{n=1}^3 \dfrac{(-1)^{n-1}}{n!}\dfrac{x^n}{n} = x-\dfrac{x^2}{4}+\dfrac{x^3}{18} \] At \(x=0.1\), this is: \[\begin{aligned} f(0.1)&\approx0.1-\dfrac{0.1^2}{4}+\dfrac{0.1^3}{18} \\ &\approx0.1-.002\,5+.000\,056 \approx .097\,556 \end{aligned}\]

    3. If you approximate \(f(0.1)\) by the Maclaurin polynomial of degree \(3\) for \(f(x)\), find a bound on the error in the approximation.

       \(\displaystyle |E_3| \lt 10^{-6}\)

       Since \(\displaystyle f(0.1)=\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n!}\dfrac{(0.1)^n}{n}\) is an alternating decreasing series, the error in truncating the series at \(n=3\) is less than the absolute value of the \(n=4\) term. \[ |E_3| \lt \left|\dfrac{(-1)^3}{4!}\dfrac{(0.1)^4}{4}\right| =\dfrac{10^{-4}}{96}\approx 10^{-6} \]

    4. Using the Maclaurin polynomial of degree \(3\) for \(f(x)\) approximate \(f(-0.1)\).

       \(\displaystyle f(0.1)\approx-0.102\,556\)

       The Maclaurin polynomial of degree \(3\) is: \[ f(x)\approx\sum_{n=1}^3 \dfrac{(-1)^{n-1}}{n!}\dfrac{x^n}{n} = x-\dfrac{x^2}{4}+\dfrac{x^3}{18} \] At \(x=-0.1\), this is: \[\begin{aligned} f(0.1)&\approx-0.1-\dfrac{0.1^2}{4}-\dfrac{0.1^3}{18} \\ &\approx-0.1-.002\,5-.000\,056 \approx-0.102\,556 \end{aligned}\]

    5. If you approximate \(f(-0.1)\) by the Maclaurin polynomial of degree \(3\) for \(f(x)\), find a bound on the error in the approximation.

       The Taylor Remainder theorem says \(|R_{k}f(x)| \le \dfrac{M}{(k+1)!}|x-a|^{k+1}\) where \(M \ge f^{(k+1)}(c)\) for \(c\) between \(a\) and \(x\).

       \(|R_{3}f(.1)| \le \dfrac{1}{96}10^{-4}\approx10^{-6}\)

       Since the series \[ f(-0.1)=\sum_{n=1}^\infty \dfrac{(-1)^{n-1}}{n!}\dfrac{(-0.1)^n}{n} =-\sum_{n=1}^\infty \dfrac{0.1^n}{n\cdot n!} \] is not alternating, we cannot use the next term to bound the error when truncating the series at \(n=3\). We must use the Taylor bound on the remainder: \[ |R_{k}f(x)| \le \dfrac{M}{(k+1)!}|x-a|^{k+1} \] where \(M \ge f^{(k+1)}(c)\) for \(c\) between \(a\) and \(x\). With \(a=0\), \(k=3\) and \(x=.1\): \[ |R_{3}f(.1)| \le \dfrac{M}{4!}|.1|^4 \] where \(M \ge |f^{(4)}(c)|\) on \([ 0,.1]\). So we need to compute \(f^{(4)}(c)\): \[\begin{aligned} f(x)&=\int_0^x \dfrac{1-e^{-t}}{t}\,dt \\ f'(x)&=\dfrac{1-e^{-x}}{x} \\ f''(x)&=\dfrac{xe^{-x}-(1-e^{-x})}{x^2}=\dfrac{xe^{-x}+e^{-x}-1}{x^2} \\ f^{(3)}(x)&=\dfrac{x^2(-xe^{-x}+e^{-x}-e^{-x})-(xe^{-x}+e^{-x}-1)2x}{x^4} \\ &=\dfrac{-x^2e^{-x}-2xe^{-x}-2e^{-x}+2}{x^3} \\ \end{aligned}\] \[\begin{aligned} f^{(4)}(x)&=\dfrac{x^3(x^2e^{-x}-2xe^{-x}+2xe^{-x}-2e^{-x}+2e^{-x})-(-x^2e^{-x}-2xe^{-x}-2e^{-x}+2)3x^2}{x^6} \\ &\qquad=\dfrac{x(x^2e^{-x})-(-x^2e^{-x}-2xe^{-x}-2e^{-x}+2)3}{x^4} \\ &\qquad=\dfrac{x^3e^{-x}+3x^2e^{-x}+6xe^{-x}+6e^{-x}-6}{x^4} \end{aligned}\]

       We need the maximum of \(|f^{(4)}(x)| \) on \([ 0,.1] \). So we plot \(|f^{(4)}(x)|\) on this interval:
       The maximum is at \(x=0\) which we compute as the limit \[ M=\lim_{x\to0}\left|\dfrac{x^3e^{-x}+3x^2e^{-x}+6xe^{-x}+6e^{-x}-6}{x^4}\right| =\dfrac{1}{4} \] Thus \[ |R_{3}f(.1)| \le \dfrac{M}{4!}|.1|^4 =\dfrac{1}{96}10^{-4}\approx10^{-6} \]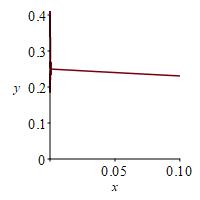

       

11. Evauate \(\displaystyle f(x)=\int_0^x \sinh(t^2)\,dt\) as a power series centered at \(x=0\). Find its radius of convergence.

    By definition: \[ \sinh x=\dfrac{e^x-e^{-x}}{2} \] Subtract the series for \(e^x\) and \(e^{-x}\).

    \(\begin{aligned} f(x)&=\int_0^x \sinh(t^2)\,dt =\sum_{k=0}^\infty \dfrac{x^{4k+3}}{(4k+3)(2k+1)!} \\ &=\dfrac{x^3}{3}+\dfrac{x^7}{7\cdot3!}+\dfrac{x^{11}}{11\cdot5!} +\dfrac{x^{15}}{15\cdot7!}+\cdots \end{aligned}\)
    \(R=\infty\)

    We start with the series: \[ e^x=\sum_{n=0}^\infty \dfrac{x^n}{n!} \quad \text{and} \quad e^{-x}=\sum_{n=0}^\infty (-1)^n\dfrac{x^n}{n!} \] When we subtract these, the terms with even values of \(n\) cancel; the terms with odd values of add up. So we write \(n=2k+1\). When we subtract and divide by \(2\), we get: \[\begin{aligned} \sinh x&=\dfrac{e^x-e^{-x}}{2} =\sum_{k=0}^\infty \dfrac{x^{2k+1}}{(2k+1)!} \\ &=x+\dfrac{x^3}{3!}+\dfrac{x^5}{5!}+\dfrac{x^7}{7!}+\cdots \end{aligned}\] (Notice how similar this is to the series for \(\sin(x)\). It's just missing the \((-1)^k\).) For this problem we now substitute \(x=t^2\): \[\begin{aligned} \sinh(t^2) &=\sum_{k=0}^\infty \dfrac{t^{4k+2}}{(2k+1)!} \\ &=t^2+\dfrac{t^6}{3!}+\dfrac{t^{10}}{5!}+\dfrac{t^{14}}{7!}+\cdots \end{aligned}\] Then we integrate \[\begin{aligned} f(x)&=\int_0^x \sinh(t^2)\,dt =\sum_{k=0}^\infty \int_0^x \dfrac{t^{4k+2}}{(2k+1)!}\,dt \\ &=\sum_{k=0}^\infty \dfrac{x^{4k+3}}{(4k+3)(2k+1)!} \\ &=\dfrac{x^3}{3}+\dfrac{x^7}{7\cdot3!}+\dfrac{x^{11}}{11\cdot5!} +\dfrac{x^{15}}{15\cdot7!}+\cdots \end{aligned}\] Since the series for \(e^x\) converges for all \(x\), so do the series for \(e^{-x}\), for \(\sinh x\), for \(\sinh(t^2)\) and for \(f(x)\). So the radius of convergence is \(R=\infty\).

12. The function \(\mathrm{Si}(x)\), called the Sine Integral function, is defined by \(\displaystyle \mathrm{Si}(x)=\int_0^x \dfrac{\sin t}{t}\,dt\).

    1. Find the Maclaurin series for \(\mathrm{Si}(x)\).

       Start with the series for \(\sin t\).

       \(\begin{aligned} \mathrm{Si}(x) &=\int_0^x \dfrac{\sin t}{t}\,dt =\sum_{k=0}^\infty (-1)^k\dfrac{x^{2k+1}}{(2k+1)(2k+1)!} \\ &=x-\dfrac{x^3}{3\cdot3!}+\dfrac{x^5}{5\cdot5!}-\cdots \end{aligned}\)

       We start with: \[ \sin t=\sum_{k=0}^\infty (-1)^k\dfrac{t^{2k+1}}{(2k+1)!} =t-\dfrac{t^3}{3!}+\dfrac{t^5}{5!}-\cdots \] Then \[ \dfrac{\sin t}{t}=\sum_{k=0}^\infty (-1)^k\dfrac{t^{2k}}{(2k+1)!} =1-\dfrac{t^2}{3!}+\dfrac{t^4}{5!}-\cdots \] And: \[\begin{aligned} \mathrm{Si}(x) &=\int_0^x \dfrac{\sin t}{t}\,dt =\sum_{k=0}^\infty \int_0^x (-1)^k\dfrac{t^{2k}}{(2k+1)!}\,dt \\ &=\sum_{k=0}^\infty (-1)^k\dfrac{x^{2k+1}}{(2k+1)(2k+1)!} \\ &=x-\dfrac{x^3}{3\cdot3!}+\dfrac{x^5}{5\cdot5!}-\cdots \end{aligned}\]

    2. Approximate \(\mathrm{Si}(0.3)\) by the Maclaurin polynomial of degree \(3\) for \(\mathrm{Si}(x)\).

       \(\displaystyle \mathrm{Si}(0.3)\approx T_3\mathrm{Si}(0.3)=.2985\)

       The Maclaurin series for \(\mathrm{Si}(x)\) is: \[ \mathrm{Si}(x) =\sum_{k=0}^\infty (-1)^k\dfrac{x^{2k+1}}{(2k+1)(2k+1)!} \] The Maclaurin polynomial of degree \(3\) is: \[ T_3\mathrm{Si}(x) =x-\dfrac{x^3}{3\cdot3!} \] At \(x=0.3\), this is: \[\begin{aligned} \mathrm{Si}(0.3) &\approx T_3\mathrm{Si}(0.3) = 0.3-\dfrac{0.3^3}{3\cdot3!} \\ &=.3-.0015 =.2985 \end{aligned}\]

    3. If you approximate \(\mathrm{Si}(0.3)\) by the Maclaurin polynomial of degree \(3\) for \(\mathrm{Si}(x)\), find a bound on the error in the approximation.

       \(\displaystyle |E_1| \lt 4\times10^{-6}\)

       Since \(\mathrm{Si}(0.3) =\sum_{k=0}^\infty \dfrac{(-1)^k}{(2k+1)}\dfrac{(0.3)^{2k+1}}{(2k+1)!}\) is an alternating decreasing series, the error in truncating the series at \(k=1\) is less than the absolute value of the \(k=2\) term. \[ |E_1| \lt \left|\dfrac{0.3^5}{5\cdot5!}\right| =.000\,004\,05\approx4\times10^{-6} \]

d. Numeric Series and Fundamental Constants

1

2

13. Use a Maclaurin polynomial for \(e^x\) to estimate \(\dfrac{1}{e}\) to within \(\pm 10^{-6}\). What degree polynomial did you need? Why?

    \(e^{-1}\approx.367\,879\)
    This required a \(9^\text{th}\) degree polynomial because the series is alternating and the \(10^\text{th}\) degree term is the first term less than \(10^{-6}\).

    The Maclaurin series for \(e^x\) is: \[ e^x=\sum_{n=0}^\infty \dfrac{x^n}{n!} \] At \(x=-1\) this becomes \[ \dfrac{1}{e}=\sum_{n=0}^\infty \dfrac{(-1)^n}{n!} =1-1+\dfrac{1}{2}-\dfrac{1}{6}+\dfrac{1}{24}-\cdots \] Since the series is alternating, we can stop when the next term is less than \(10^{-6}\). Since \(10!=3\,628\,800 \gt 10^6\) we can stop at \(9\) terms. So: (Use a calculator to add them up.) \[ e^{-1}\approx \sum_{n=0}^9\dfrac{(-1)^n}{n!} =.367\,879 \]

14. Approximate \(\pi\) as follows:

    1. Use the equation \(\displaystyle \arctan\left(\dfrac{1}{\sqrt{3}}\right) =\dfrac{\pi}{6}\) to derive the formula \(\displaystyle \pi=2\sqrt{3}\sum_{n=0}^\infty \dfrac{(-1)^n}{2n+1}\left(\dfrac{1}{3}\right)^n\).

       The Maclaurin series for \(\arctan x\) is \[ \arctan x =\sum_{n=0}^\infty \dfrac{(-1)^n}{2n+1}x^{2n+1} \] So \[\begin{aligned} \pi&=6\arctan\left(\dfrac{1}{\sqrt{3}}\right) =6\sum_{n=0}^\infty \dfrac{(-1)^n}{2n+1}\left(\dfrac{1}{\sqrt{3}}\right)^{2n+1} \\ &=2\sqrt{3}\sum_{n=0}^\infty \dfrac{(-1)^n}{2n+1}\left(\dfrac{1}{3}\right)^n \end{aligned}\]

    2. Use the \(4^\text{th}\) partial sum for this series to approximate \(\pi\).

       \(\displaystyle \pi\approx2\sqrt{3}\sum_{n=0}^4 \dfrac{(-1)^n}{2n+1}\left(\dfrac{1}{3}\right)^n =3.142\,60\)

       \[\begin{aligned} \pi &=2\sqrt{3}\sum_{n=0}^\infty \dfrac{(-1)^n}{2n+1}\left(\dfrac{1}{3}\right)^n \approx2\sqrt{3}\sum_{n=0}^4 \dfrac{(-1)^n}{2n+1}\left(\dfrac{1}{3}\right)^n \\ &=2\sqrt{3}\left[1-\dfrac{1}{3\cdot3}+\dfrac{1}{5\cdot9} -\dfrac{1}{7\cdot27}+\dfrac{1}{9\cdot81}\right] \\ &=3.464\,10\left[1-.111\,11+.022\,22-.005\,29+.001\,37\right] \\ &=3.142\,60 \end{aligned}\]

    3. Find a bound on the error in this approximation.

       \(\displaystyle |E_4| \lt 0.0013\)

       Since the series \(\displaystyle 2\sqrt{3}\sum_{n=0}^\infty \dfrac{(-1)^n}{2n+1}\left(\dfrac{1}{3}\right)^n\) is alternating, the error is less than the absolute value of the next term, the \(n=5\) term: \[ |E_4| \lt 2\sqrt{3}\dfrac{1}{11\cdot243} =0.0013 \]

       Our approximation for \(\pi\) was \(\pi\approx3.142\,60\) and the error in this approximation was \(|E_4| \lt 0.0013\). So the actual value must satisfy \(3.142\,60-.0013 \lt \pi \lt 3.142\,60+.0013\) or \(3.1413 \lt \pi \lt 3.1439\). In fact, to \(5\) digits, \(\pi\approx 3.1416\).

e. Differential Equations

1

15. Consider the initial value problem: \[ \dfrac{dy}{dx}=x^2y \qquad \text{with} \qquad y(3)=2 \]

    1. Find the quadratic Taylor polynomial centered at \(x=3\), for the solution to this initial value problem.

       The quadratic Taylor polynomial about \(x=3\) has the form: \[ T_2y(x)=y(3)+y'(3)(x-3)+\dfrac{1}{2}y''(3)(x-3)^2 \] So we need to find \(y(3)\), \(y'(3)\) and \(y''(3)\).

       \(\displaystyle T_2y(x)=2+18(x-3)+87(x-3)^2\)

       The quadratic Taylor polynomial about \(x=3\) has the form: \[ T_2y(x)=y(3)+y'(3)(x-3)+\dfrac{1}{2}y''(3)(x-3)^2 \] So we need to find \(y(3)\), \(y'(3)\) and \(y''(3)\). From the initial condition and the differential equation, we have: \[\begin{aligned} y(3) &=2 \\ y'(3) &=[x^2y]_{(x,y)=(3,2)}=3^2 2=18 \end{aligned}\] Next we implicitly differentiate the differential equation: \[ \dfrac{d^2y}{dx^2} =\dfrac{d}{dx}(x^2y) =2xy+x^2\dfrac{dy}{dx}=2xy+x^4y \] Hence: \[ y''(3)=[ 2xy+x^4y]_{(x,y)=(3,2)} =2\cdot3\cdot2+3^4\cdot2=174 \] So: \[ T_2y(x)=2+18(x-3)+87(x-3)^2 \] (Don't forget the \(\dfrac{1}{2}\) in the quadratic term.)

    2. This differential equation is separable. Find the exact solution to the initial value problem, \(y=f(x)\).

       \(\displaystyle y=f(x)=2e^{x^{\scriptsize 3}/3-9}\)

       We separate the equation and integrate: \[\begin{aligned} \int \dfrac{1}{y}\,dy&=\int x^2\,dx \\ \ln|y|&=\dfrac{x^3}{3}+C \\ |y|&=e^{x^{\scriptsize 3}/3+C} \\ y&=Ae^{x^{\scriptsize 3}/3} \quad \text{where}\; A=\pm e^C \end{aligned}\] When \(x=3\), we have \(y=2\). So \[ 2=Ae^{3^{\scriptsize 3}/3}=Ae^9 \Longrightarrow A=2e^{-9} \] Therefore the solution is: \[ y=f(x)=2e^{x^{\scriptsize 3}/3-9} \]

    3. Find the quadratic Taylor polynomial centered at \(x=3\), for the exact solution, \(y=f(x)\), to this initial value problem.

       The quadratic Taylor polynomial about \(x=3\) has the form: \[ T_2f(x)=f(3)+f'(3)(x-3)+\dfrac{1}{2}f''(3)(x-3)^2 \] So we need to find \(f(3)\), \(f'(3)\) and \(f''(3)\).

       \(\displaystyle T_2f(x)=2+18(x-3)+87(x-3)^2\)

       The quadratic Taylor polynomial about \(x=3\) has the form: \[ T_2f(x)=f(3)+f'(3)(x-3)+\dfrac{1}{2}f''(3)(x-3) ^2 \] So we need to find \(f(3)\), \(f'(3)\) and \(f''(3)\). Here is a table of the function and its first two derivatives and their values at \(x=3\): \[\begin{aligned} f(x)&=2e^{x^{\scriptsize 3}/3-9} &f(3)&=2e^{3^{\scriptsize 3}/3-9}=2 \\ f'(x)&=2x^2e^{x^{\scriptsize 3}/3-9} &f'(3)&=2\cdot3^2e^{3^{\scriptsize 3}/3-9}=18 \\ f''(x)&=4xe^{x^{\scriptsize 3}/3-9}+2x^4e^{x^{\scriptsize 3}/3-9} &f''(3)&=4\cdot3e^{3^{\scriptsize 3}/3-9}+2\cdot3^4e^{3^{\scriptsize 3}/3-9} =174 \end{aligned}\] So the quadratic Taylor series about \(x=3\) is: \[ T_2f(x)=2+18(x-3)+87(x-3)^2 \] which is the same as we got using a Taylor series to solve the differential equation.

16. Consider the initial value problem: \[ \dfrac{dy}{dx}=x+y \qquad \text{with} \qquad y(1)=4. \]

    1. Find the quadratic Taylor polynomial centered at \(x=1\), for the solution to this initial value problem.

       The quadratic Taylor polynomial about \(x=1\) has the form: \[ T_2y(x)=y(1)+y'(1)(x-1)+\dfrac{1}{2}y''(1)(x-1)^2 \] So we need to find \(y(1)\), \(y'(1)\) and \(y''(1)\).

       \(\displaystyle T_2y(x)=4+5(x-1)+3(x-1)^2\)

       The quadratic Taylor polynomial about \(x=1\) has the form: \[ T_2y(x)=y(1)+y'(1)(x-1)+\dfrac{1}{2}y''(1)(x-1)^2 \] So we need to find \(y(1)\), \(y'(1)\) and \(y''(1)\). From the initial condition and the differential equation, we have: \[\begin{aligned} y(1) &=4 \\ y'(1) &=[x+y]_{(x,y)=(1,4)}=1+4=5 \end{aligned}\] Next we implicitly differentiate the differential equation: \[ \dfrac{d^2y}{dx^2} =\dfrac{d}{dx}(x+y) =1+\dfrac{dy}{dx} =1+x+y \] Hence: \[ y''(3)=[1+x+y]_{(x,y)=(1,4)} =6 \] So: \[ T_2y(x)=4+5(x-1)+3(x-1)^2 \] (Don't forget the \(\dfrac{1}{2}\) in the quadratic term.)

    2. This differential equation is linear. Find the exact solution to the initial value problem, \(y=f(x)\).

       \(\displaystyle y=f(x)=6e^{x-1}-x-1\)

       The standard form of the equation is: \[ \dfrac{dy}{dx}-y=x \] We identify \(P(x)=-1\). So the integrating factor is \[ I=e^{\int(-1)\,dx}=e^{-x} \] We multiply the standard equation by the integrating factor and identify the left side as a derivative of a product: \[\begin{aligned} e^{-x}\dfrac{dy}{dx}-e^{-x} y&=xe^{-x} \\ \dfrac{d}{dx}(e^{-x} y)&=xe^{-x} \end{aligned}\] Next we integrate. (The integral on the right needs an integration by parts. Check it by differentiating.) \[ e^{-x} y=\int xe^{-x}\,dx=-(x+1)e^{-x}+C \] To find \(C\), we use the initial condition, when \(x=1\), we have \(y=4\): \[ e^{-1} 4=-(2)e^{-1}+C \Longrightarrow C=6e^{-1} \] So the implicit solution is: \[ e^{-x} y=-(x+1)e^{-x}+6e^{-1} \] and the explicit solution is: \[ y=f(x)=-(x+1)+6e^{x-1}=6e^{x-1}-x-1 \]

    3. Find the quadratic Taylor polynomial centered at \(x=1\), for the exact solution, \(y=f(x)\), to this initial value problem.

       The quadratic Taylor polynomial about \(x=1\) has the form: \[ T_2f(x)=f(1)+f'(1)(x-1)+\dfrac{1}{2}f''(1)(x-1)^2 \] So we need to find \(f(1)\), \(f'(1)\) and \(f''(1)\).

       \(\displaystyle T_2f(x)=4+5(x-1)+3(x-1)^2\)

       The quadratic Taylor polynomial about \(x=1\) has the form: \[ T_2f(x)=f(1)+f'(1)(x-1)+\dfrac{1}{2}f''(1)(x-1)^2 \] So we need to find \(f(1)\), \(f'(1)\) and \(f''(1)\). Here is a table of the function and its first two derivatives and their values at \(x=1\): \[\begin{aligned} f(x)&=6e^{x-1}-x-1 &f(1)&=6-1-1=4 \\ f'(x)&=6e^{x-1}-1 &f'(1)&=6-1=5 \\ f''(x)&=6e^{x-1} &f''(1)&=6 \end{aligned}\] So the quadratic Taylor series about \(x=1\) is: \[ T_2f(x)=4+5(x-1)+3(x-1)^2 \] which is the same as we got using a Taylor series to solve the differential equation.

Review Exercises

17. Compute \(\displaystyle \lim_{x\to0}\dfrac{\cos x-1+\dfrac{x^2}{2}}{x^4}\)

    \(\displaystyle \lim_{x\to0} \dfrac{\cos x-1+\dfrac{x^2}{2}}{x^4}=\dfrac{1}{24}\)

    We substitute the series: \(\displaystyle \cos x=1-\dfrac{x^2}{2}+\dfrac{x^4}{24}-\cdots\) into the limit and simplify: \[\begin{aligned} \lim_{x\to0} &\dfrac{\cos x-1+\dfrac{x^2}{2}}{x^4} \\ &=\lim_{x\to0} \dfrac{\left(1-\dfrac{x^2}{2}+\dfrac{x^4}{24}-\cdots\right)-1+\dfrac{x^2}{2}}{x^4} \\ &=\lim_{x\to0} \dfrac{\;\dfrac{x^4}{24}-\cdots\;}{x^4} =\dfrac{1}{24} \end{aligned}\]

18. The error function is defined by \(\displaystyle \mathrm{erf}(x) =\dfrac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\,dt\)

    1. Find the Maclaurin series for \(\mathrm{erf}(x)\).

       \(\displaystyle \mathrm{erf}(x)=\dfrac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\,dt =\sum_{n=0}^\infty \dfrac{2}{\sqrt{\pi}}\dfrac{(-1)^n}{(2n+1)n!}x^{2n+1}\)

       Substitute \(x=-t^2\) into the series: \[ e^x=\sum_{n=0}^\infty \dfrac{x^n}{n!} \] to get: \[ e^{-t^2}=\sum_{n=0}^\infty \dfrac{(-t^2)^n}{n!} =\sum_{n=0}^\infty \dfrac{(-1)^n}{n!}t^{2n} \] Then \[\begin{aligned} \mathrm{erf}(x) &=\dfrac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\,dt \\ &=\dfrac{2}{\sqrt{\pi}}\sum_{n=0}^\infty \dfrac{(-1)^n}{n!}\int_0^x t^{2n}\,dt \\ &=\dfrac{2}{\sqrt{\pi}}\left.\sum_{n=0}^\infty \dfrac{(-1)^n}{n!}\dfrac{t^{2n+1}}{2n+1}\right|_0^x \\ &=\sum_{n=0}^\infty \dfrac{2}{\sqrt{\pi}}\dfrac{(-1)^n}{(2n+1)n!}x^{2n+1} \end{aligned}\]

    2. Approximate \(\mathrm{erf}(1)\) by the Maclaurin polynomial of degree \(5\) for \(\mathrm{erf}(x)\).

       \(T_5\mathrm{erf}(1) =\dfrac{23}{15\sqrt{\pi}} \approx.865\)

       We approximate the series: \[ \mathrm{erf}(x)=\dfrac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\,dt =\dfrac{2}{\sqrt{\pi}}\sum_{n=0}^\infty \dfrac{(-1)^n}{(2n+1)n!}x^{2n+1} \] by \[\begin{aligned} T_5\mathrm{erf}(x) &=\dfrac{2}{\sqrt{\pi}}\sum_{n=0}^2 \dfrac{(-1)^n}{(2n+1)n!}x^{2n+1} \\ &=\dfrac{2}{\sqrt{\pi}}\left(x-\dfrac{x^3}{3}+\dfrac{x^5}{5\cdot2}\right) \end{aligned}\] Then at \(x=1\) we have: \[\begin{aligned} T_3\mathrm{erf}(1) &=\dfrac{2}{\sqrt{\pi}}\left(1-\dfrac{1}{3}+\dfrac{1}{10}\right) =\dfrac{23}{15\sqrt{\pi}} \approx.865 \end{aligned}\]

    3. Find a bound on the error in this approximation.

       \(|E_2| \lt .027\)

       Since the series \(\displaystyle \mathrm{erf}(1) =\dfrac{2}{\sqrt{\pi}}\sum_{n=0}^\infty \dfrac{(-1)^n}{(2n+1)n!}\) is alternating, the error is bounded by the absolute value of the next term, i.e. the \(n=3\) term: \[ |E_2| \lt \dfrac{2}{\sqrt{\pi}}\dfrac{1}{(7)3!} =\dfrac{1}{21\sqrt{\pi}} \approx.027 \]

       Our approximation for \(\mathrm{erf}(1)\) was \(T_5\mathrm{erf}(1)\approx.865\) and the error in this approximation was \(|E_2| \lt .027\). So the actual value must satisfy \(.865-.027 \lt \mathrm{erf}(1) \lt .865+.027\) or \(.838 \lt \mathrm{erf}(1) \lt .892\). In fact, to \(7\) digits, \(\mathrm{erf}(1)\approx .8427008\).

PY: All Checked